|
| 1 | +# 756. Pyramid Transition Matrix |
| 2 | +You are stacking blocks to form a pyramid. Each block has a color, which is represented by a single letter. Each row of blocks contains **one less block** than the row beneath it and is centered on top. |
| 3 | + |
| 4 | +To make the pyramid aesthetically pleasing, there are only specific **triangular patterns** that are allowed. A triangular pattern consists of a **single block** stacked on top of **two blocks**. The patterns are given as a list of three-letter strings `allowed`, where the first two characters of a pattern represent the left and right bottom blocks respectively, and the third character is the top block. |
| 5 | + |
| 6 | +* For example, `"ABC"` represents a triangular pattern with a `'C'` block stacked on top of an `'A'` (left) and `'B'` (right) block. Note that this is different from `"BAC"` where `'B'` is on the left bottom and `'A'` is on the right bottom. |
| 7 | + |
| 8 | +You start with a bottom row of blocks `bottom`, given as a single string, that you **must** use as the base of the pyramid. |
| 9 | + |
| 10 | +Given `bottom` and `allowed`, return `true` *if you can build the pyramid all the way to the top such that **every triangular pattern** in the pyramid is in* `allowed`*, or* `false` *otherwise*. |
| 11 | + |
| 12 | +#### Example 1: |
| 13 | +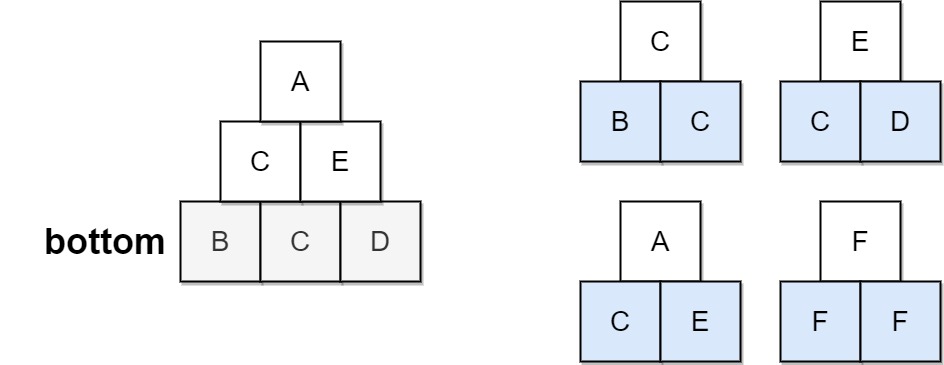 |
| 14 | +<pre> |
| 15 | +<strong>Input:</strong> bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"] |
| 16 | +<strong>Output:</strong> true |
| 17 | +<strong>Explanation:</strong> The allowed triangular patterns are shown on the right. |
| 18 | +Starting from the bottom (level 3), we can build "CE" on level 2 and then build "A" on level 1. |
| 19 | +There are three triangular patterns in the pyramid, which are "BCC", "CDE", and "CEA". All are allowed. |
| 20 | +</pre> |
| 21 | + |
| 22 | +#### Example 2: |
| 23 | +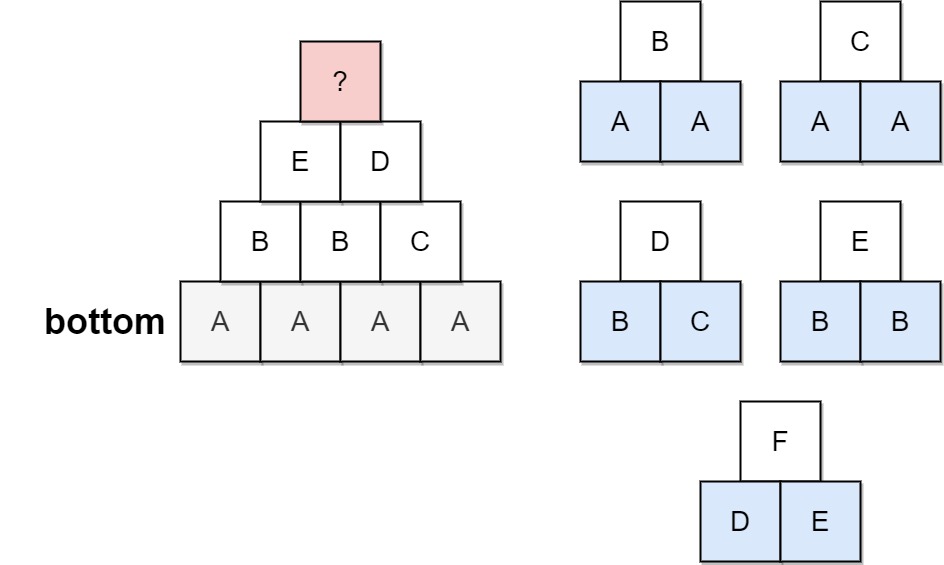 |
| 24 | +<pre> |
| 25 | +<strong>Input:</strong> bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"] |
| 26 | +<strong>Output:</strong> false |
| 27 | +<strong>Explanation:</strong> The allowed triangular patterns are shown on the right. |
| 28 | +Starting from the bottom (level 4), there are multiple ways to build level 3, but trying all the possibilites, you will get always stuck before building level 1. |
| 29 | +</pre> |
| 30 | + |
| 31 | +#### Constraints: |
| 32 | +* `2 <= bottom.length <= 6` |
| 33 | +* `0 <= allowed.length <= 216` |
| 34 | +* `allowed[i].length == 3` |
| 35 | +* The letters in all input strings are from the set `{'A', 'B', 'C', 'D', 'E', 'F'}`. |
| 36 | +* All the values of `allowed` are **unique**. |
| 37 | + |
| 38 | +## Solutions (Python) |
| 39 | + |
| 40 | +### 1. Solution |
| 41 | +```Python |
| 42 | +class Solution: |
| 43 | + def pyramidTransition(self, bottom: str, allowed: List[str]) -> bool: |
| 44 | + @cache |
| 45 | + def buildFromBottom(bottom: str) -> bool: |
| 46 | + if len(bottom) == 1: |
| 47 | + return True |
| 48 | + |
| 49 | + top = [''] * (len(bottom) - 1) |
| 50 | + |
| 51 | + def buildTop(i: int) -> bool: |
| 52 | + if i >= len(top): |
| 53 | + return buildFromBottom(''.join(top)) |
| 54 | + |
| 55 | + for pattern in allowed: |
| 56 | + if bottom[i:i + 2] == pattern[:2]: |
| 57 | + top[i] = pattern[2] |
| 58 | + if buildTop(i + 1): |
| 59 | + return True |
| 60 | + top[i] = '' |
| 61 | + |
| 62 | + return False |
| 63 | + |
| 64 | + return buildTop(0) |
| 65 | + |
| 66 | + return buildFromBottom(bottom) |
| 67 | +``` |
0 commit comments